The 'Special' menu contains several utility
functions, calculators, and converters.
Most 'Special' menu calculators have a 'Print Window Image' button near the bottom of the window. This sends a copy of the window contents to either a printer or to a graphics file (pdf, png, etc.).
 SIMPLE MATH calculator This is
a basic calculator with some additional keys that are specific to data acquisition. Along with standard math operations, it contains keys for time unit or rate conversions (multiplying and dividing by factors of 60 and 24), pressure (760, 101.325, etc.), Kelvin temperature, and a number of surface and volume conversions frequently used by physiologists and other scientists. SIMPLE MATH calculator This is
a basic calculator with some additional keys that are specific to data acquisition. Along with standard math operations, it contains keys for time unit or rate conversions (multiplying and dividing by factors of 60 and 24), pressure (760, 101.325, etc.), Kelvin temperature, and a number of surface and volume conversions frequently used by physiologists and other scientists.
The calculator has an RPN function with addition, subtraction, multiplication, and division (which should be familiar to users of HP desk calculators). Note that you should use the underline key (_) instead of the minus key (-) for subtraction (this is because the minus key is assumed to indicate a negative number, not subtraction).
Also note that when computing sines, cosines, or tangents, the calculator expects angles in degrees (not radians).
SIMPLE REGRESSION calculator This window lets you perform simple linear or 2-order polynomial regressions. It is not intended to replace the much more sophisticated regression algorithms found in dedicated statistics packages: it doesn't provide a lot of the standard regression statistics, and there is an upper limit of 20 X-Y variable pairs (you need to enter at least three). Once the data are entered, clicking the 'Calculate Regression' button computes and displays the regression coefficients and shows a plot of the data and regression line:
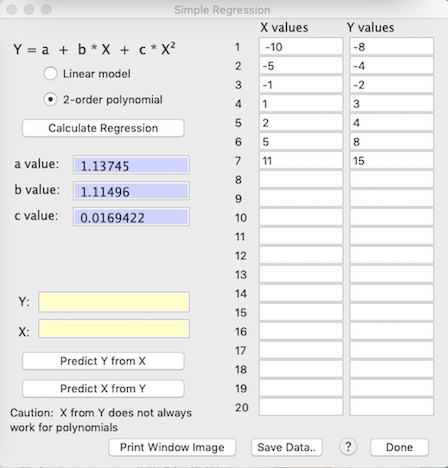
- Once a regression has been computed, you can use the 'Predict Y from X' and 'Predict X from Y' buttons to interpolate values (but note that predicting X from Y does not always work in polynomial regressions).
- The X and Y values will be remembered if you close this window and subsequently re-open it (but are lost when you quit LabHelper).
• EXPRESSION EVALUATOR...
This routine lets you write a mathematical expression,
enter numeric values for the expression variables, and have the computer
solve it for X and (optionally) Y values. The program parses the expression into components and performs
the operations.

The expression evaluator understands the following
symbols (upper or lower case entries are OK):
- Simple operators: + - * / ^ ( )
- Complex operators: EXP, LOG or
LN, LOG10, SIN, COS, TAN, ATN or ATAN, ABS, INT, SQR (square), SQRT (square
root)
- Two special variables (i.e., channels) named "X" and
"Y", chosen with push-buttons (see image below)
- PI (or the equivalent Greek letter)
- Numbers (such as 5, -3.1889, and
1e-10)
- You can add a comment at the end of your expression, delineated
with the " ` " character.
Some general considerations:
- You can store and retrieve up to 4 expressions using the 'Retrieve Expression x' and 'Store as Expression x' popup menus. This will save the trouble (and error potential) of re-entering frequently-used expressions at each use.
- The 'Check expression' button does a preliminary parsing of
the expression and indicates if there are any syntax errors (in the above
example, this button has been clicked).
- The 'Evaluate' button processes the expression using the X and Y values you entered. If any errors are found (see below), a warming message is shown.
NOTE: This routine will only 'catch'
errors in the basic numeric expression. It may
not detect invalid or meaningless math operations that may be attempted
when data are processed, such as division by zero, or taking the
log or a non-integer exponent of a negative number. If such situations
occur, results may be unpredictable.
| |