RUNNING AVERAGE...
Lets you click on a series of SINGLE points
while LabAnalyst X keeps track of the
cumulative mean, standard deviation (SD), coefficient of variation (CV),
and standard error (SE). The program also shows the summed total of
all selected points, and the range (minimum and maximum values).
To select points for analysis, move the cursor to the point of interest
in the plot area and click once. Then move to the next point and repeat.
- You can eliminate a single mistake (the last point indicated
with a mouse click) with the delete key.
- To exit the routine, move the cursor to the RESULTS window and click
the mouse once (the cursor can be anywhere in the result window).
- NOTE: this operation DOES NOT highlight the results window title bar
when active, as shown in this example.
PAIRS DIFFERENCE... Calculates
the cumulative mean, SD, and SE of a series of PAIRS of points. You
select point pairs with mouse clicks (an example might be the peaks and
valleys of a ventilation trace). LabAnalyst
X measures the absolute difference between the points in the
pair. It also calculates the cumulative mean, SD, and SE of the time
intervals between points. As for RUNNING AVERAGE, the delete
key gets rid of the last pair of points selected.
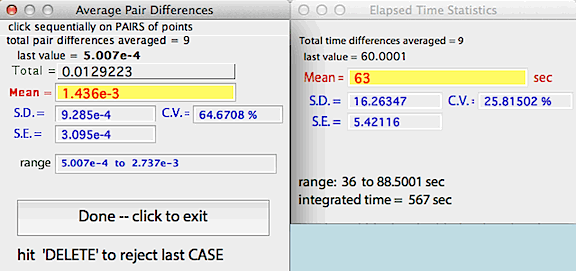
NOTE: this operation DOES NOT highlight the results window title when
active, as can be seen in the example above.
back to top
If a data block HAS been selected,
you can perform the following operations:
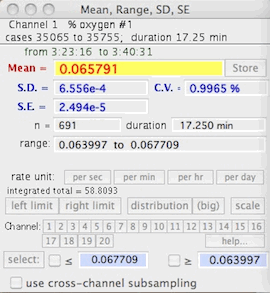
BASIC STATS
Computes the mean, range, standard
deviation (SD), standard error (SE), and coefficient of variation (CV) of
the block (it also shows the time duration and the data range).
To get the integrated total for a rate function, such as oxygen consumption,
make sure the correct rate unit is selected (i.e., 'per min' if the
units are ml/min or 'per hour' if the units are ml/hour). A more sophisticated
integration mode is available in the INTEGRATE
BLOCK option.
Use the 'limits' buttons to restrict analysis to a subsection
of the block (move the cursor to the block window and click when the limit
line is correctly positioned).
The 'scale' button toggles scaling of the results (see SCALE RESULTS, below). The 'Store'
button in this and other analysis mode windows allows you to directly transfer
the current mean for use as a scaling factor. When you click 'Store',
the scaling factors window appears. Click on any channel's "*"
or "÷" button, and the current mean will appear in the
first edit field (the multiplication or division factor) for that channel.
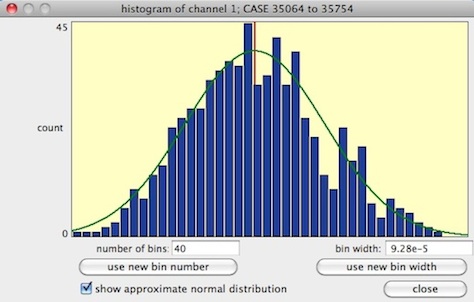
The 'distribution' button produces a small bar graph of frequency distribution.
If the file has more than one channel, you can click on buttons for different
channels and get those means (you can also use the keyboard to select channels). The (big) button shows a much larger and more detailed distribution:
back to top
MINIMUM VALUE...
M
MAXIMUM VALUE...
MOST LEVEL...
MOST VARIABLE...
Allow you to enter an interval (in seconds) and LabAnalyst
X will search within the selected block for either the highest
or lowest continuous average over that interval, or the most level
or most variable region within the block.
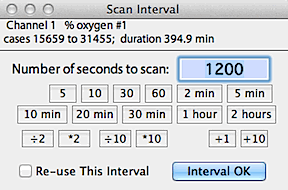Activating the 'reuse this interval' button
in the interval selection window will bypass the interval selection routine
during subsequent uses of these analyses (such as when using the AUTOREPEAT
option for new blocks).
For the MOST LEVEL option, the 'most level' region is the interval
in which the sum of absolute differences from the interval mean (i.e.,
the sum of Xi - meanX,
or point-to-point variance) is lowest. Note that this is not necessarily
the interval with the lowest slope, although this usually turns out to be
the case.
For the MOST VARIABLE option, you can select to search either
for the region with maximum overall slope or the region with maximum
point-to-point variance.
When your interval selection is complete, click
the 'interval OK' button and the program will find the appropriate
interval and display the results in the next window, shown below.
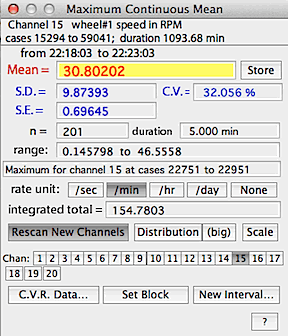
After calculations, the maximal, minimal, or most level area is shown
as a color-inverted rectangle on the block window.
As for BASIC STATS, you can switch to other channels, but in the
default mode the interval boundaries remain constant -- i.e., the same beginning
and ending points as on the initially scanned channel are used for other
channels. This sounds confusing but it allows you to scan for the
period of, say, lowest VO2 and then get
the temperature, CO2, etc. for that
specific period.
Alternately, you can activate the 'rescan new channels' button
to force a re-scan of each new channel selected.
Two other considerations:
- Rate units, distribution plots, storing data, and scaling are as described
for BASIC STATS.
- The 'Set block' button turns the sub-block (minimum, maximum,
etc.) into the selected block for use in other analyses.
When using the MINIMUM VALUE... and MAXIMUM VALUE...
functions, a button labeled 'C.V.R. data...' is available.
This stands for Constant Volume Respirometry, and it
opens a window that lets you set up the variables needed to compute O2 or CO2 exchange
in a closed system. Note that this option assumes that the data being
analyzed are in units of % gas concentration and that baseline has already
been corrected.
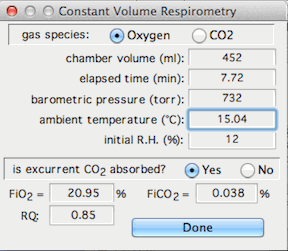
You need to specify the gas type, the chamber volume, the elapsed time,
the chamber temperature, the barometric pressure, the initial relative humidity
in the chamber (if the gas contains water vapor), the initial concentrations
of O2 and CO2
(FiO2 and FiCO2),
and the respiratory exchange ratio (RQ). You also need to specify
whether or not CO2 is absorbed prior to
oxygen analysis ('excurrent CO2' buttons). When done, click
the 'Selection OK' button.
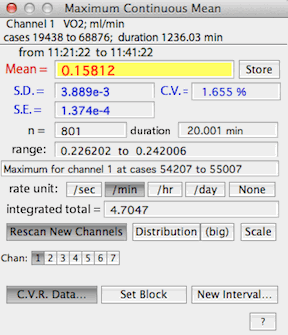
When C.V.R. options is activated, the results window (example
on the right) shows gas exchange rates in units of ml/min -- but note that
only the mean value is computed as gas
exchange (the SD, SE, etc. are shown in their original units).
To switch off the C.V.R. calculations, click the 'C.V.R.
data...' button.
back to top
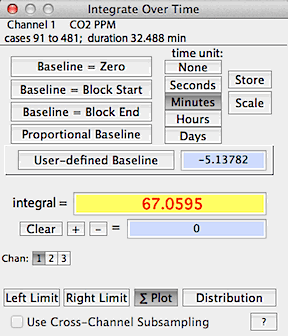
INTEGRATE BLOCK...
Finds the area under the curve
within the defined block.
There is a choice of time units (seconds, minutes, hours, days, none)
and baseline values. The baseline for integration can be set at zero,
the initial value of the block, the final value of the block,
a user-specified value, or a proportional linear correction
between initial and final block values. Because of the different baseline
options, this operation is considerably more versatile than the integration
feature including in BASIC STATS, MINIMUM, MAXIMUM, and LEVEL.
In this example, the block is integrated using the zero baseline
option with the time unit set as minutes. Note that the start, end,
and proportional options apply to the block defined with the left and
right limit functions.
Keep in mind that you need to pick the time unit that matches the rate
unit used in the channel being analyzed, or the results will not be valid.
If you are using a rate unit for which a matching time unit is not available,
you will need to adjust the results manually. For example,
if your data are in units of Kilojoules/day, you will need to divide the
results by the factorial difference between days and whatever unit you select.
To continue with this example, if you set the units to 'hours' and
your data are in KJ/day, you must divide the results by 24 (since there
are 24 hours per day). Similarly, if you set the units to 'minutes',
you would need to divide by the number of minutes per day (1440).
This can be done conveniently using the 'Store'
and 'Scale' buttons.
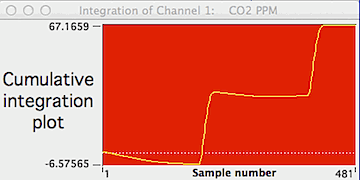If you select the "Integration plot"
option (button in the bottom row), the computer generates a plot of the
integrated values over time. This plot will change whenever a new
channel, right or left limit, or baseline option is selected.
Additional considerations:
- Use the '+', '-', and 'clear' buttons to add or subtract
successive integral measurements.
- Use the 'limits', 'store', and 'scale' buttons as described
for BASIC STATS.
This operation DOES NOT print to a tabular file (the output format isn't
compatible since there are no SDs or SEs generated during integration).
back to top
LabAnalyst X
contains three methods of analyzing the cyclical or waveform
structure of a data set. These are the WAVEFORM, TIME
SERIES, and FFT (fast Fourier transform) operations. All
have different approaches, and the best one to use depends largely on the
data set in question.
WAVEFORM... 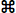W Uses simple
algorithms to calculate wave frequency and mean peak height. Basically,
the program looks for successive 'peaks' and 'valleys' in
the data. A peak (the 'crest' of a waveform) is defined as a series
of 5 points with the middle point having the highest value, and with values
declining in the two points on either side. The inverse is true for
a valley (the 'trough' of a waveform). LabAnalyst
X marks the peaks and valleys it finds with dotted (valleys)
or dashed (peaks) lines in the block window (see below).
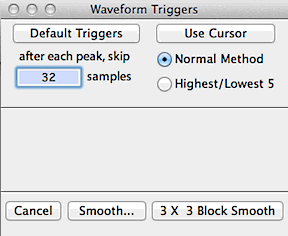
In the default mode the program will use all the data within the block.
Alternately, 'filtering' is possible through cursor selection of minimum
peak and valley values ('triggers') in the block window. Click
the 'use cursor' button and move the cursor to the block window.
A horizontal line will track the cursor's movement and a readout in the
Results window will show the height of the cursor. Click once
to select a peak (done first) or valley trigger. After selection,
peak triggers are shown as pink lines, and valley triggers are green lines.
The post-peak trigger value (default zero) is the number of cases
the program 'skips' after finding a peak. This option can be useful
when analyzing noisy files.
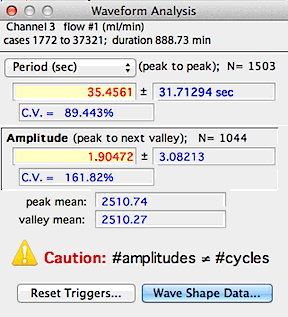
A typical results window is shown at right, above. Note that in
this example the number of periods and amplitudes is correctly matched.
The program beeps and prints a warning if no periodicity is found, if no
amplitudes are found, or if the number of amplitudes does not equal the
number of cycles +1 (indicating that some peaks were not associated with
definable valleys, so the frequency or amplitude may be incorrect).
The mean values for both peaks and valleys are also shown.
back to top
NOTE: The waveform algorithms are easily confused by noise (because
of the way peaks and valleys are defined). If you are only interested
in frequency, it is reasonably safe to reduce noise by smoothing data prior to analysis.
However, smoothing reduces peak amplitudes (in some cases very dramatically),
so it must be used with caution if you need peak height data. Smoothing
is least damaging if peaks are 'rounded' and contain many more points than
the smoothing interval. If necessary, use PAIRS
DIFFERENCE to obtain peak heights, then obtain frequency data after
smoothing.
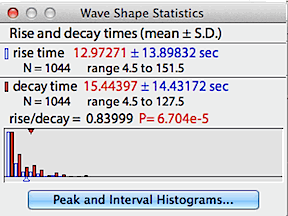The 'wave shape data' button opens a window
with statistical information on the waveform's rise and decay times.
Rise time (the elapsed time from a valley to a subsequent peak) is shown
in blue; decay time (the elapsed time from a peak to a subsequent valley)
is shown in red. The small triangles indicate the means while the
bars show the distributions.
If the data contain more than 10 peaks, additional analyses are available
from the Peak and interval histograms button, which produces histograms
of peak height (shown as the absolute value), wave amplitude
(valley to peak) and interpeak interval (essentially the wavelength
calculated on a peak-to-peak basis). An example is shown below.
The save data button stores a text file of the histogram values,
the print graph button sends the data to a printer, and the square-root
Y button shows the count as a square-root, which better shows bars with
low counts.
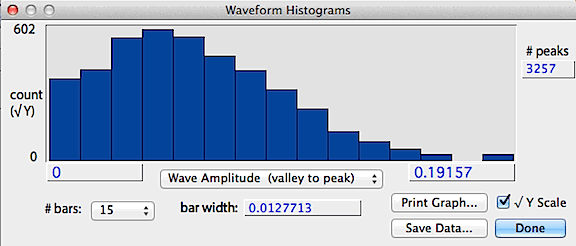
back to top
Time
series 
This
submenu has two items:
BASIC TIME SERIES... This
option displays time series data in graphical form. Time series analysis
examines data for many kinds of temporal relationships -- basically, does
sample value at a particular time (T) predict sample value at some
later time (T + z)? A graphical display is useful for determining
if there are periodicities within the data, and (if periodicities exist)
if the waveforms are symmetrical. When this option is selected, LabAnalyst X opens a window containing edit
fields for the Start Lag (the initial time increment between samples)
and the Time Step (the time increment added for each successive
plot). Defaults are a start lag of 0 and a time step of 1 sample.
Edit as desired. There are two plotting options.
Use the 'Plot time series' button to generate 18 scatterplots.
For each, the sample value (X - coordinate) is plotted against the sample
value at a fixed time increment in the future (Y -coordinate):
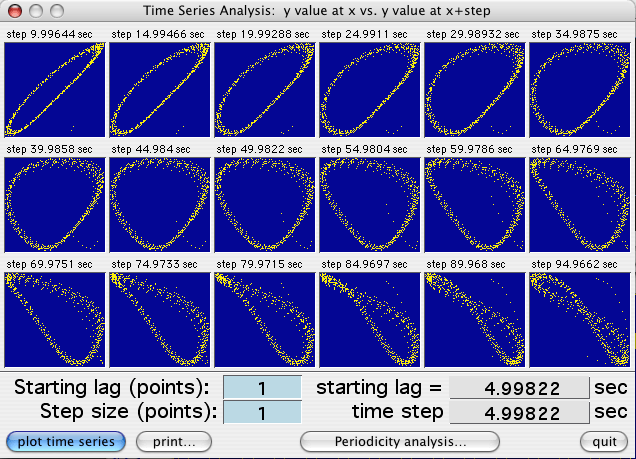
In each plot the time increment is equal to the
start lag plus the sum of the cumulative time steps (i.e., start lag +
time step X plot number). The increment value is shown at the top
of each plot. If there is no temporal predictability, the point distribution
will be random. However, if temporal patterns exist, the distribution
of points will be non-random, and the shape of the distribution will indicate
the degree of symmetry and the scatter will indicate the degree of randomness
or 'noise'. You can replot with different start lags and time step
increments. Click the 'Print plots' button for hard-copy output.
Note that 24, not 18, time steps are plotted, and that you cannot
select this button until data have been plotted on the screen.
This is the setup screen for generating a periodicity test plot:
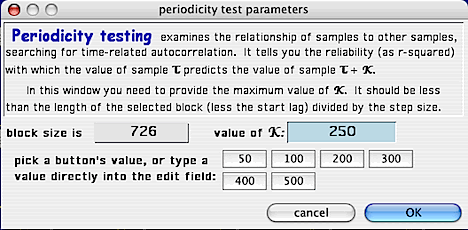
Use one of the 'value' buttons, or enter a value directly, to generate a summarized 'periodicity
test' for however many stepped time intervals you want (NOTE: these buttons
are only available if there are sufficient points within the block -- assuming
a start lag of 1 and a time step of 1).
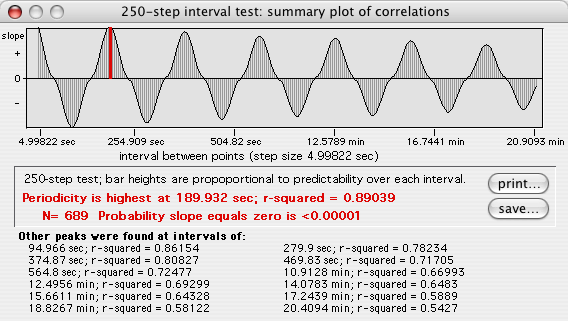
This example shows a 250-step plot. Correlations with negative
slopes are plotted below the zero line. Bar heights are a relative
index of how value at time (T) predicts value at time (T
+ time step). The tallest bar (red on color screens) is the interval
with highest predictability.
Click the 'Print' button for hard-copy output; click the 'Quit'
button, another window, or the close box to return to the analysis page.
back to top
STEPPED SAMPLING...
This routine computes, plots, and saves sequentially sampled data at user-set
intervals; among other uses, this helps determine the degree to which data
sampled at one time are correlated to data sampled at different times (i.e.,
autocorrelation). For example, if you wanted to compute a relationship
between (say) voluntary running speed and metabolism from a file containing
many different running speeds, you would need to obtain your measurements
at large enough intervals so that there was no autocorrelation between
measurements. The intuitive expectation is that successive measurements
obtained at very short intervals will closely resemble each other, but
eventually become independent as the interval between measurements increases.
The goal would be to use an inter-measurement interval large enough to
be sure that autocorrelation ('pseudoreplication') is minimal.
The iterative sampling process starts at an initial point (a particular
sample) in the file, then steps forwards and backwards by user-defined
intervals (the 'skip' interval) and takes the mean, range, and SD of blocks
of data of user-set duration, symbolized as:
-------||||||||-------|||||||--------|||||||-------||||||||-------
where ----- = skipped samples, ||||| = blocks, and | is
the initial point
This process is repeated until user-defined limits are reached, or the
start of end of the data are reached. The initial point can be a user-set
sample number or the central point in a data block (for example, you could
search for the highest point in a data file, use the 'set block'
option, and then use the resulting block as the initial point). If a block
is selected, the start and end points are set to the beginning and ending
points of the block. The default value is 1/2 of the total number of samples.
The control window looks like this:
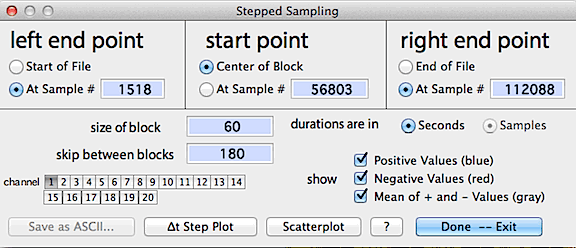
When ready, click either the "delta-t step plot" button
or select a new channel to display results, as in the following example:
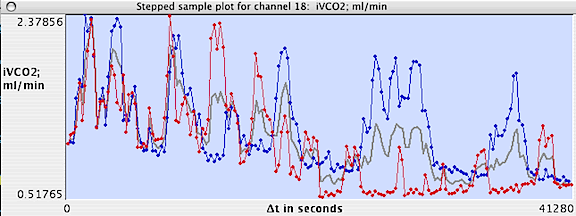
Results are plotted on-screen (blue
for measurements later than the initial point, red
for measurements earlier than the initial point, and gray
for the mean value for both + and - values at a given interval).
The 'scatterplot' button shows an X-Y scatterplot of step-sampled
data from any two of the available channels (it's only available if there
are 2 or more channels in the file).
You can use the channel buttons to select up to 10 channels that can
be analyzed and stored in a tab-delineated (Excel compatable)
file with the "save as ASCII" button. Note that you can
select more than 10 channels, but only results from the first 10 will be
stored. If the file contains interpolated data as indicated with the standard
interpolation markers "»" and "«", any
stored values that were computed from interpolated data will be marked
in the Excel file.
back to top
FFT...
Uses a Fast Fourier Transform (FFT) to calculate
the frequency structure of cyclic data. Theoretically, any waveform
can be decomposed into a set of simple sine waves of different frequencies
and phases. The FFT algorithm finds these fundamental frequencies
and displays them as peaks in the plot area.
Complex 'summed' frequency data occur frequently in
biology (and in other areas of science). For example, you might want
to use an impedance converter to measure the heart rate in a small mammal,
bird, or lizard. Unfortunately, in addition to heart rate, you will
also pick up signals produced by breathing movements. Therefore the
instrument output will contain a confusing summation of the combined effects
of breathing and heart rate. It may also contain 'noise' from random
or irregular events (such as muscle movement from minor postural adjustments).
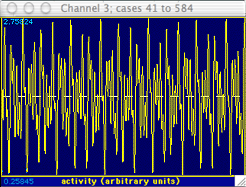
The messy-looking data shown at right are an example of such a waveform.
Although it is obviously complex, a visual inspection suggests that it does
contain some regularity. However, this periodicity is not readily
studied with either the WAVEFORM or TIME SERIES operations.
Fortunately, the FFT procedure can help find the important underlying components
of this complex wave. In many cases it can detect basic cycles in
a data set even if they are visually 'buried' by random noise.
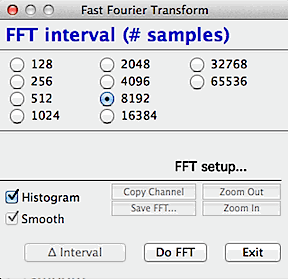The first step in the FFT procedure
is selection of the size of the block of data to be analyzed. The
FFT algorithm requires that the block size be a power of two; depending
on the size of your data set you can select any block size from 128 samples
up to a maximum of 262,144 (256K) samples (in this example, the total number of
samples in the file was about 700; accordingly, the largest possible block
for FFT analysis is 512 samples).
After you select a block size, the program will show the block duration
and then prompt you to go to the plot window and select the block to be
analyzed. Do this by moving the cursor into the plot area, where it
will outline a block of the size you selected. Fit the cursor block
over the subset of data you wish to analyze and click the mouse once.
This will select the desired FFT block.
Once the block is chosen, you can proceed transform it (Do FFT button),
select another block size (by clicking the appropriate 'power of two' button),
or exit. You may choose between showing a line or
histogram plot of the results, and whether or not the results are smoothed.
After completing the FFT, the waveform's fundamental frequencies are
shown graphically in the plot area. You can examine the details of
this structure by moving the cursor over the plot; the fundamental frequencies
that have been 'decomposed' from the original signal, and their amplitudes,
are shown numerically as peaks in the results window.
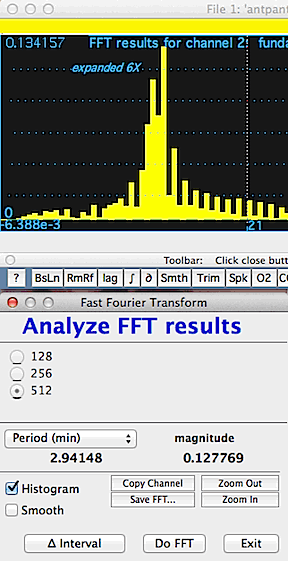In this example, the waveform from the first image
(above) is seen to be composed of three discrete fundamental frequencies,
which appear as the three sharp peaks in the plot area. The cursor
is over one of the peaks, which has a frequency of 5.2757 Hz and a magnitude
(useful for comparisons among peaks) of .7146 (these data are displayed
in the results window). You have a choice of
output units (frequency in Hz, kHz, etc.; period in sec, min, etc.)
After the transform is complete, you can expand or shrink
the display, or smooth (or unsmooth) the data (the results in this
example are smoothed).
FFT results are stored in channel zero (not normally used by LabAnalyst X); use the copy button to
move them to a 'regular' data channel if you want to save them to disk(copying
is only possible if the number of 'regular' channels is <24). In the
latest versions, you can use the print button to produce an Excel-compatable
spreadsheet containing the frequency data (in whatever units you select)
and amplitudes.
Note that if you click the exit button, you are transferred to
the plot area window in channel zero (which contains the FFT results).
If you click the close box you are transferred back to the original
data channel. If you chose the former, you can switch back to the
regular channels by pushing the appropriate number key, or clicking the
channel selection buttons in the upper right corner of the plot area.
You cannot get back to the FFT results in channel zero except by
re-running the FFT procedure.
Note that if you start the FFT procedure while using the multi-channel
display mode, you'll be switched to single-channel mode (using the current
active channel) prior to the beginning of analyses. At the conclusion
of the FFT calculations you'll be returned to multi-channel mode IF
you click the close box or (in FP versions) the plot area.
back to top
SLOPE vs TIME...
Calculates rates of change over time within a data
block. Seconds, minutes, hours, or days may be selected as the time
units. You may use a linear (least-squares) regression or a semi-log
regression (log Y = a + b*time).
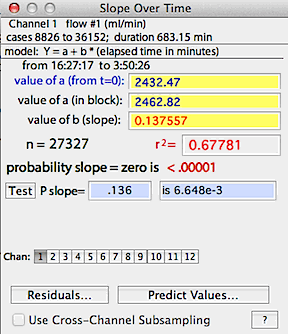
When the calculations are complete, a regression line is superimposed
on the block window. The program computes slope, r-squared, and probabilities
that the slope is either one or zero.
Two values of 'a' (the intercept) are given. One is based on the
time change calculated from the start of the file (t=zero), and the other
is based on the time change within the block, using the assumption that
time zero is the start of the block.
You can switch channels (for new calculations) with the usual selection
buttons on the bottom of the results window. To change the time units,
re-select the original channel.
You can also test the slope against any user-defined value with the 'test'
button.
Some additional considerations:
- Note that in SLOPE and REGRESSION you cannot send results
to disk or printer by hitting the 'p' key, as usual. Instead, use
the 'print' button (this button only appears if output has been
selected from the FILE menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
REGRESS CHANNELS...
This option performs basic regression
analysis for any two channels (obviously, it is only available if the file
has more than one channel):
The initial step in the regression procedure is
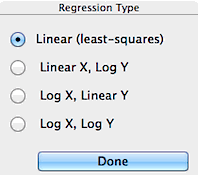
to chose the type of unit conversions. Linear (least-squares),
semi-log (log Y = a+b*X or Y = a+b*log X), and log-log (log
Y = a + b*log X) regression models are available. However, some of
the conversions will not be available if the data range includes zero or
negative values (since one can't take the log of a negative number).
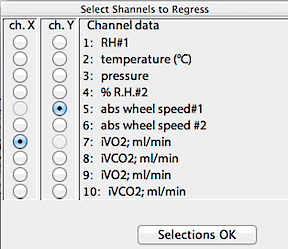
Next, you select the two channels to regress, using the window shown
at right. The program won't let you attempt to regress a channel against
itself, so you may have to do some fancy button-clicking to get your channels
selected.
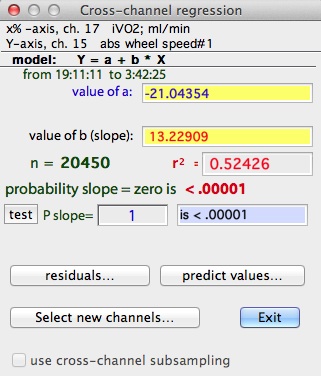After the 'selections OK' button is clicked, LabAnalyst
X performs the calculations and produces a scatterplot of the
data points in the block window (x values versus y values), along with the
regression line.
The numerical results are the same as for the SLOPE vs TIME option
described above -- except that only a single value of the intercept is shown.
You can test the slope against any user-defined value. Enter the slope
into the edit field and click the 'test' button (very low probability
values are shown as "<.00001").
The 'residuals' button will produce a scatterplot of residuals from the regression. 'Select new channels' lets you set up a new regression of different variables.
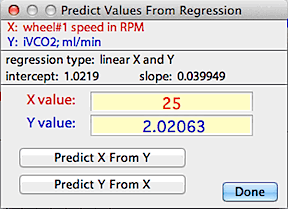You can use the 'predict values' button to use
the regression equation to predict X from a given Y, or vice versa:
Some additional considerations:
- Note that in SLOPE and REGRESSION you cannot send results
to disk or printer by hitting the 'p' key, as usual. Instead, use
the 'print' button (this button only appears if output has been
selected from the FILE menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
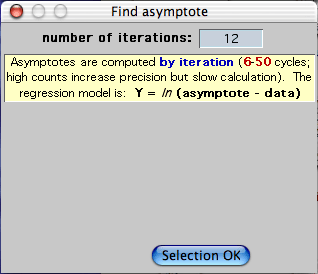
FIND ASYMPTOTE...
This is an application of first-order kinetics, in which data approach a
stable plateau (asymptote) according to a rate constant (this means
that the fractional rate of approach to the asymptote is constant
over time). Some examples include heating and cooling (the "Newtonian"
model) and gas mixing and washout characteristics (and many other physical
phenomena).
The program uses an iterative method to find the best-fit asymptote for
a selected block of data, according to the simple model: Y = ln(asymptote
- data). You can chose any number of iterations between 6 and
50. Using a lot of iterations might increase the accuracy of
the estimate (this doesn't always occur), but will also increase the analysis
time. In practice, you usually don't need to use more than 6 to 10
iterations for good accuracy. Note that if you give it 'messy' data
that do not conform reasonably well to first-order kinetics, the program
may take a long time to produce an estimate (and that estimate may have
fairly glaring errors).
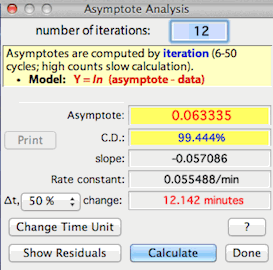
After completing the analysis, LabAnalyst X
shows the asymptote, the coefficient of determination or C.D.
(an estimate of the precision of the fit of the data to the model, and hence
the precision of the estimated asymptote), the slope of the ln-transformed
data, the rate constant (the fraction of the change between a
starting value and the asymptote that is completed during 1 time unit),
and the time to complete a fraction of the total change between a starting
value and the asymptote (values from 1% to 99% are selectable from a pop-up
menu). You can use your choice of time units (seconds, minutes, hours,
or days) for slopes and rate constants.
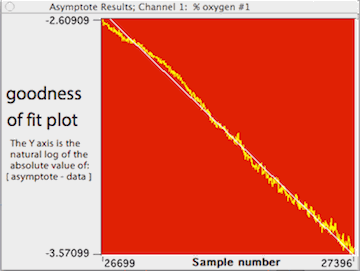LabAnalyst X
also draws a goodness-of-fit plot that illustrates how closely the model
matches the data. Points are plotted in yellow as the log (base e) of the
absolute difference between the model predictions and the data:
Y value = ln(abs(asymptote - data))
Individual points are shown only if the total number of points in the
plot is less than 60. The line predicted by the model is shown in white.
In this example (not the same as for the previous figure), the analysis
contained 31 points ranging in value from about 31.1 to slightly less than
0, with a predicted asymptote of -0.05. You can also plot the residuals
from this regression.
Some additional considerations:
- The time needed for finding an asymptote increases with the size of
the data block (as well as the number of iterations). On a fast machine
running the FP version of the software, a block containing several thousand
data points will be analyzed within a few seconds. On slower machines
with older versions, analysis can take considerably
longer.
- You cannot send results to disk or printer by hitting the 'p' key,
as usual. Instead, use the 'print' button (this button
is available only if output has been selected from the FILE
menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
FIT POLYNOMIAL... In some cases,
relationships between different variables are best expressed with a polynomial
regression. LabAnalyst X lets
you fit pairs of channels with polynomials of up to 9 degrees. The
model is: Channel Y = (polynomial expression of Channel X).
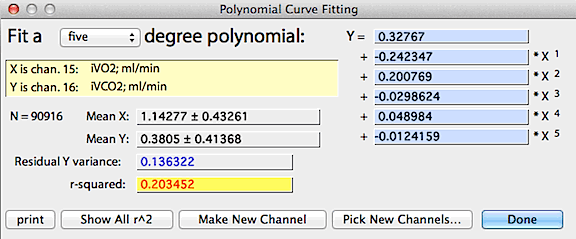
After you select the X and Y channels (as described above for linear regression), the program
computes and displays a default polynomial of 3 degrees. You can then
select other degrees using the pop-up menu. In this example, a 6-degree
polynomial was used to predict CO2 concentration
from oxygen concentration; the resulting equation -- shown at the right
of the window -- explains 99% of the variance in % CO2.
After completing the analysis, several options are available. The
'select new channels' button lets you change the X and Y variables.
The 'make new chan from polynomial' button (only available if the
number of channels is less than 24) generates a new channel by applying
the current polynomial equation to the data in the X channel -- in other
words, it computes and saves a new Y value for every sample in the X channel.
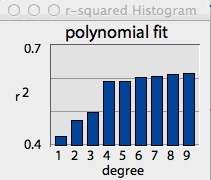The 'show all r^2' button helps you select
the most appropriate degree for the polynomial equation. The predictive
value of a polynomial always increases as the degree increases.
However, the increase in accuracy usually plateaus, so it is reasonable
to use the simplest equation consistent with good predictive power.
When the 'show all r^2' button is clicked, the program computes the
r2 value for all degrees between 1 and 9, and then shows a bar
graph of the results. [You can remove this plot by clicking the highlighted
'show all r^2' button.]
In the example shown at right, there was little change in predictive
power until the degree of the polynomial exceeded 3, and then little additional
change until the degree reached 8 and 9 (you can select the color of bar
graph plots in the Colors and
lines option in the VIEW menu.)
Some additional considerations:
- In some conditions (particularly if you are computing a high-degree
polynomial when the magnitudes of the X and Y channels differ greatly),
it is possible to exceed the numeric limits of the program. Usually,
the value of r-squared is set to zero when this happens.
- You cannot send results to disk or printer by hitting the 'p' key,
as usual. Instead, use the 'print' button (this button
is available only if output has been selected from the FILE
menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
TIME INTEGRATION
This operation calculates the cumulative
duration of data in the selected block that satisfy two Boolean criteria:
greater than one user-selected value, and less than a second user-selected
value.
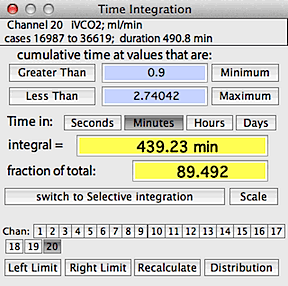
An example time integration window is shown at right. The default
minimum and maximum values are the lower and upper limits (respectively)
of the data range in the block, which includes 100% of the data and results
in a single event in each category. You can set new limits (as shown
here) in three ways:
- When the 'minimum' or 'maximum' buttons are clicked,
the limits are reset to these values
- When the 'greater than' or 'less than' buttons are clicked,
you can use the mouse to move cursor in the block window to graphically
select the upper and lower limits.
- Finally, you can directly type in the limit values in the edit fields
(hitting "return" will force the program to recalculate the results).
- Be sure to select the time unit you want. Some additional considerations
include:
- You cannot send results to disk or printer by hitting the 'p' key,
as usual. Instead, use the 'print' button (this button
only appears if output has been selected from the FILE
menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
EVENT COUNTING
This operation counts the number of 'events'
in the selected block that satisfy two Boolean criteria: greater than
one user-selected value, and less than a second user-selected value.
An 'event' occurs when the data cross one of the two Boolean 'boundaries'.
A 'negative' event is counted when the data drop below the lower
limit, and a 'positive' event is counted when the data rise above
the upper limit.
An example of event counting is shown below. The default minimum
and maximum values are the lower and upper limits (respectively) of the
data range in the block, which includes 100% of the data and results in
a single event in each category.
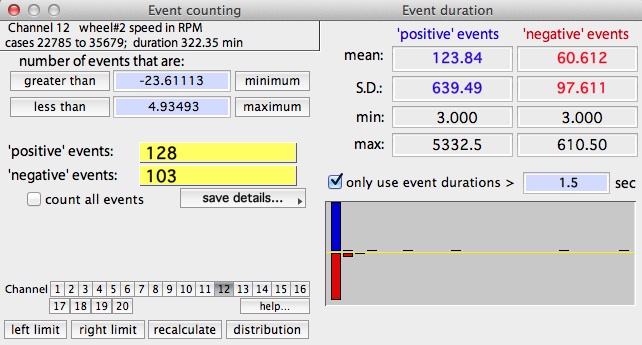
You can set new limits in three ways:
- When the 'minimum' or 'maximum' buttons are clicked,
the limits are reset to these values
- When the 'greater than' or 'less than' buttons are clicked,
you can use the mouse to move cursor in the block window to graphically
select the upper and lower limits.
- Finally, you can directly type in the limit values in the edit fields
(hitting "return" will force the program to recalculate the results).
- You can include all the events, or elect to analyze only events longer than a minimum duration. Toggle these options with the 'count all events' button.
Some additional considerations include:
- You cannot send results to disk or printer by hitting the 'p' key,
as usual. Instead, use the 'print' button (this button
only appears if output has been selected from the FILE
menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
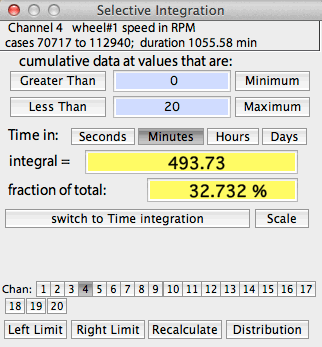
SELECTIVE INTEGRATION
This operation integrates all data in
the selected block that satisfy two Boolean criteria: greater than one user-selected
value, and less than a second user-selected value. The window shows
the integrated value in absolute terms and as the fraction of the total
integrated block.
An example of selective integration is shown at right. The default
minimum and maximum values are the lower and upper limits (respectively)
of the data range in the block, which includes 100% of the data and results
in a single event in each category. You can set new limits (as shown
here) in three ways:
- When the 'minimum' or 'maximum' buttons are clicked,
the limits are reset to these values
- When the 'greater than' or 'less than' buttons are clicked,
you can use the mouse to move cursor in the block window to graphically
select the upper and lower limits.
- Finally, you can directly type in the limit values in the edit fields
(hitting "return" will force the program to recalculate the results).
- Some additional considerations include:
- You cannot send results to disk or printer by hitting the 'p' key,
as usual. Instead, use the 'print' button (this button
only appears if output has been selected from the FILE
menu).
- This option DOES NOT print to a tabular file (the output format is
incompatible).
back to top
Analysis utilities This
submenu has four items:
AUTOREPEAT R Toggles the auto-repetition feature
for analysis modes. When active, autorepeat mode repeats the last
analysis used whenever a new block is selected. If you want to do
something different, just pick the new analysis from the menu or from the
buttons below the plot area.
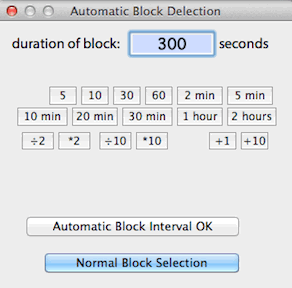
BLOCK WIDTH...
Allows automatic selection of
blocks of user-defined duration with a single mouse click, instead of the
normal method of clicking on both the start and end of the desired block.
In this mode, the cursor is contained within a box that 'frames' the block
duration in the plot area. Position the cursor over the desired block
and click once to select it.
The default automatic block size is equivalent to 13 samples or 12 sample
intervals (e.g., 60 seconds with a 5-second sample interval). Any
other block size can be selected, as long as it contains more than 2 samples
and less than 1/2 of the file duration.
Return to the standard two-click selection method with the 'Normal
block selection' button.
SCALE RESULTS... Opens
a window for entry of scaling factors that can be selectively applied to
the results of several analysis operations with the 'scale' button
(in the RESULTS window). These factors take the form:
final value = (result x B) +A or final value = (result ÷
B) +A
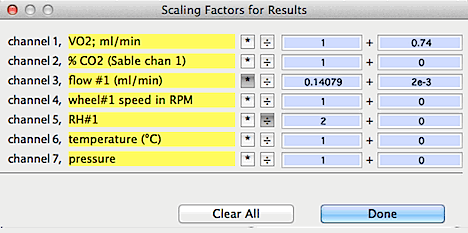Different A and B values can be
applied to each channel, but you must enter the correct values in any channel
you wish to scale (in other words, if you have scaling factors entered
for channel 5, they apply only to channel 5 unless they are also
entered in another channel of interest).
This example shows:
- addition of .74 to channel 1
- multiplication of channel 3 by 0.140479, and addition of .002 to the
result.
- division of channel 5 by 2.
- no change to the other channels.
The 'Store' button in many
of the analysis mode windows allows you to directly transfer the current
results mean for use as a scaling factor. When you click the Store
button, the scaling factors window appears. Click on any channel's
"*" or "÷" button, and the current mean will
appear in the first edit field (the multiplication or division factor)
for that channel.
back to top
DON'T USE INTERPOLATED DATA
If this option is selected, the AVERAGE,
MINIMUM VALUE, MAXIMUM VALUE, MOST LEVEL, MOST
VARIABLE, SLOPE OVER TIME, and REGRESSION operations will
not use interpolated data when scanning for desired values. Note that it
does not matter which channel was interpolated: if this option is
selected all data from any channel within interpolation boundaries
will be rejected. Note that interpolation is determined from the standard
interpolation markers: "»" indicates the start of interpolation
and "«" indicates the end of interpolation. These are optionally
set automatically in the Remove references and Interactive spike
removal operations, or you can insert them manually from the 'markers'
submenu in the VIEW menu.
If you have selected this option and an
analysis operation encounters interpolated data within the regions selected
for analysis, this warning window is shown:
You will also notice that the number of cases shown in the 'Results'
window is less than shown in the 'Block' window. The difference is the
number of interpolated data points that were ignored during analysis.
BLOCK SHIFT LEFT << ( If there is room in the plot area, this will shift the block to the left (i.e., towards earlier events) by one blockwidth of data points.
BLOCK SHIFT RIGHT >> ) If there is room in the plot area, this will shift the block to the right (i.e., towards later events) by one blockwidth of data points.
BLOCK SHIFT RULES Specifies the exact position of a new block selected with 'shift right' or 'shift left'; specifically, is there no overlap or overlap of a single point.
